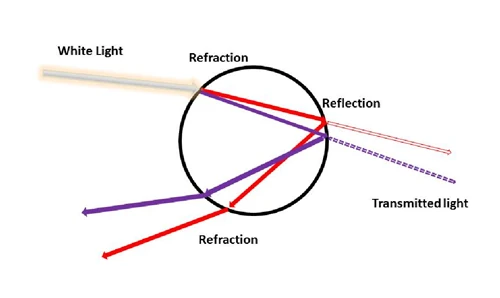
Rainbows mesmerize as the ultimate art of light to human eyes, where solar rays undergo refraction, reflection, and dispersion in water droplets at sharp 42° angles, thereby decomposing the incident white light into the six spectral ROYGBIV bands due to the wavelength-dependent bending.
Primary bows are the result of a single internal reflection, while the secondary ones arise from double bounces and Alexander’s dark band, which is the unlit sky between the two, all being regulated by Snell’s law and minimum deviation calculus, according to the explanation of the phenomena by the science.
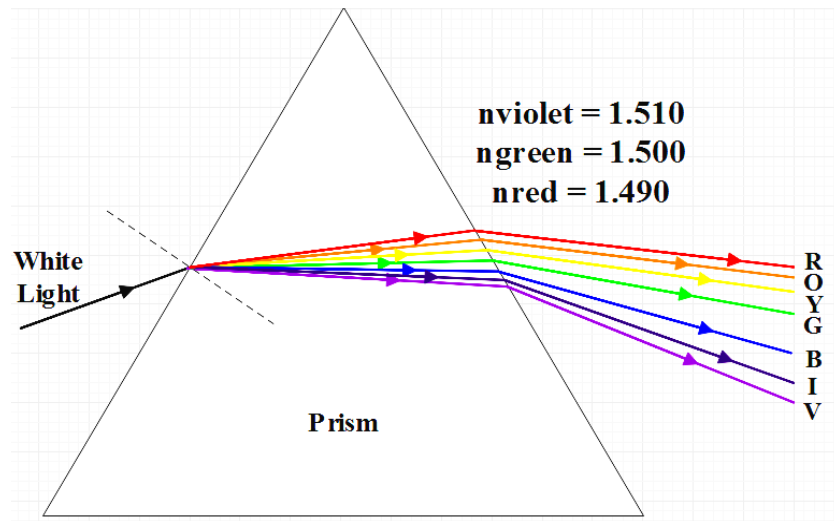
According to the scientific explanation, the process starts with sunlight getting into spherical raindrops (0.5–5 mm diameter) at low angles right after a shower. Refraction obeying Snell’s law takes place with violet bending the most (n1.343) and red the least (n1.332), thereby splitting white light into the spectrum.
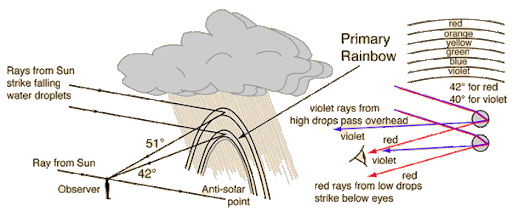
The internal total reflection is at the back of the drop (incidence >48.6); thus, the rays are directed to the observer’s side, and the exit refraction further separates the colors. Red is seen at 42.4 and violet at 40.6 from the antisolar point.
The best geometry ensures that the rays meet at the minimum deviation (Dmin=2+4D_{\min} = \pi, 2\alpha + 4\betaDmin=2+4, 59.4\alpha \approx 59.4^\circ59.4) is the one that gives the brightness; in fact, each drop behaves like a full spectrometer and produces full ROYGBIV, but the observer only sees red rays from the higher drops and violet rays from the lower ones, and thus a 42 radius arc is formed. The sun has to be less than 42 in altitude for the rainbow to be visible, which is the reason behind the appearance of the rainbow’s ephemeral post-storm magic.
Dispersion Mechanics in How Rainbows Form Science
Dispersion is the main factor in the formation of rainbows in science: shorter wavelengths refract more when entering water (sin i / sin r = n()), thus spreading the beam into a fan before reflection recombines it minus losses. Prisms do the same, but rainbows’ curved geometry from countless drops results in a continuous arc instead of a triangular spectrum. How rainbows work: science calculations give angular width ~2 dD/d=0 at extremum, with supernumerary bows from droplet-size interference adding faint inner arcs to the primary. Atmospheric purity strengthens the color, while pollution scatters the blues, thereby dimming the rainbow colors.
Primary Rainbow Geometry: How Rainbows Form Science Precision
Primary rainbows are the result of light undergoing one internal reflection in the water droplet, with the rays deviating 138 in total (2r + 180, 4i); thus, the brightest spot is at 42 radius where d(deviation)/di=0 and the flux concentrates. The red outer side and the violet inner one correspond to the wavelength ordering; a viewer below the antisolar point sees a segment that matches elevation. How rainbows form: science requires a screen of uniform drops ~50 m away, with the sun behind the shoulder; horizontally oriented drops give flattened bottoms, and fogbows from tiny particles become broader and white. Calculations (β=cos−1n2−1n3\beta = \cos^{-1} \frac{\sqrt{n^2-1}}{n\sqrt{3}}β=cos−1n3n2−1) predict exact radii, verified empirically.
Secondary Rainbows: Double Reflection in How Rainbows Form Science
Secondaries form via two internals (deviation ~231), inverting colors (violet out, red in) at 51 radius, fainter (10x less light) with wider bands from path losses. Alexander’s dark band (8 wide) between appears dim as primaries scatter inward and secondaries outward, starving intermediate angles of rays.
How rainbows form: science for secondaries mirrors primaries, but doubled bounce narrows viable incidence, requiring larger drops; lunar versions glow faintly under full moons. Glory (small aureole opposite the sun) adds via backscattering from ~0.1 mm drops.
Atmospheric Conditions for How Rainbows Form: Science Magic
For rainbows to form scientifically, one needs a specific setting: the sun should be low (less than 42), the observer should be facing the edge of the storm with the drops falling towards them, and there should be no crosswinds that might shear the alignment. Altocumulus can give partials, and virga yields none; spray fountains create “horizontal” arcs from ground reflection.
Altitude increases how scientifically visible rainbows are (higher antisolar point), while polarization (90 to plane) helps filters; double rainbows require a steady moderate rain. Climate changes may affect the frequency through storm patterns.
Myths, Math, and Modern How Rainbows Form: Science Insights
Aristotle erred in claiming celestial vapors; Descartes first modeled refraction geometrically, and Newton added dispersion, explaining colors. Modern science on how rainbows form uses ray-tracing software simulating supernumeraries, confirming Airy/Young interference for fine fringes inside primaries.
Calculus derives rainbow angle R=π−Dmin≈42∘R = \pi – D_{\min} \approx 42^\circR=π−Dmin≈42∘ from dD/di=0, n(λ) yielding spectral spread. Cultural myths (pots o’ gold, bridges to gods) persist, but how rainbows form science demystifies as elegant optics celebrating light’s wave-particle dance.
-RITOBROTA BANERJEE
MUST READ: Durgapur Horror: Another Reminder of India’s Unfinished Battle for Women’s Safety

